Lernaufgabe 9: Spulen und Kondensatoren
Hier findest du die Aufgaben ohne Lösungen.
Aufgabe 1
Ein Heizwiderstand, der an eine Gleichspannungsquelle angeschlossen wird, wandelt elektrische Energie in Wärme um. Schaltet man den Heizwiderstand an eine Wechselspannung, zeigt er die gleiche Wirkung.

Berechne den Wert des Widerstandes und der Leistung, die am Widerstand umgesetzt wird.
geg: \(I=4,6\ A, U=230\ V\)
ges: \(R, P\)
Lös:
\(R=\frac{U}{I}=\frac{230\ V}{4,6\ A}=50\ \Omega\)
\(P=U\cdot I=230\ V\cdot 4,6\ A=1058\ W\)
Antw: Der Widerstand hat einen Wert von \(50\ \Omega\) und setzt eine Leistung von \(1058\ W\) um.
Aufgabe 2
Eine Schützspule K ist zunächst an eine Gleichspannungsquelle angeschlossen. Schließt man anschließend die gleiche Schützspule an eine Wechselspannungsquelle deren Effektivwert genauso groß ist wie die Spannung der Gleichspannungsquelle, misst man nur noch eine geringere Stromstärke.
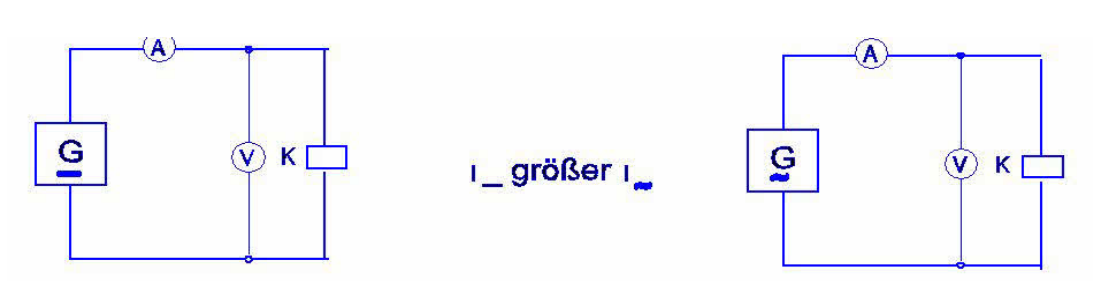
Begründe, wodurch diese Wirkung entsteht.
Die Wirkung entsteht durch den zusätzlichen Widerstand \(X_L\) (induktiver Blindwiderstand, auch Induktanz genannt).
Aufgabe 3
Ein Kondensator mit der Kapazität \(C\) wird zunächst an eine Gleichspannungsquelle angeschlossen. Dabei fließt nur solange ein Strom, bis der Kondensator aufgeladen ist. Wird dagegen der Kondensator an eine Wechselspannungsquelle mit der gleichen Quellenspannung angeschlossen, ist ein ständig fließender Strom zu messen.

Begründe, wodurch diese Wirkung ensteht.
Die Wirkung entsteht durch den zusätzlichen Widerstand \(X_C\) (kapazitiver Blindwiderstand, auch Reaktanz genannt).
Aufgabe 4
Im Bild sind 4 Spulen mit unterschiedlicher Induktivität abgebildet. Diese können wie ohmsche Widerstände zu Reihen-, Parallel- oder Gemischtschaltungen geschaltet werden.
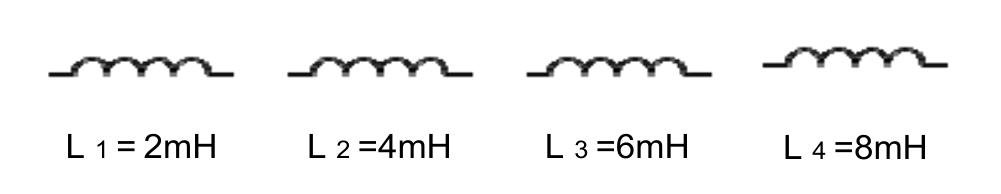
Berechne folgende Gesamtinduktivitäten \(L_\mathrm{ges}\)
1) \(L_1, L_2, L_3\) in Reihe
\(L_\mathrm{ges}=L_1+L_2+L_3=2\ mH+4\ mH+6\ mH=12\ mH\)
2) \(L_1,L_2,L_3\) parallel zueinander
\(\frac{1}{L_\mathrm{ges}} =\frac{1}{L_1}+\frac{1}{L_2}+\frac{1}{L_3}=\frac{1}{2\ mH}+\frac{1}{4\ mH}+\frac{1}{6\ mH}\)
\(=\frac{6}{12\ mH}+\frac{3}{12\ mH}+\frac{2}{12\ mH}=\frac{6+3+2}{12\ mH}=\frac{11}{12\ mH}\)
\(\Leftrightarrow L_\mathrm{ges}=\frac{12}{11}\ mH=1,09\ mH\)
3) \(L_4\) in Reihe mit der Parallelschaltung von \(L_1, L_2, L_3\)
\(L_\mathrm{ges}=L_4+1,09\ mH=8\ mH+1,09\ mH=9,09\ mH\)
Aufgabe 5
Im Bild sind 4 Kondensatoren mit unterschiedlicher Kapazität abgebildet. Diese können wie ohmsche Widerstände zu Reihen-, Parallel- oder Gemischtschaltungen geschaltet werden. Alle Werte haben die Einheit \(\mu F\)
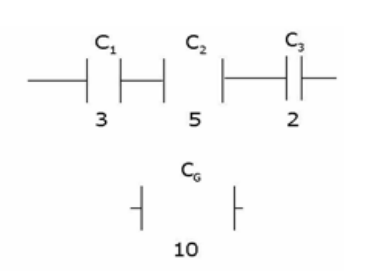
Berechne folgende Gesamtkapazitäten \(C_\mathrm{ges}\)
1) \(C_1, C_2, C_3\) in Reihe
\(\frac{1}{C_\mathrm{ges}} =\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}=\frac{1}{3\ \mu F}+\frac{1}{5\ \mu F}+\frac{1}{2\ \mu F}\)
\(=\frac{10}{30\ \mu F}+\frac{6}{30\ \mu F}+\frac{15}{30\ \mu F}=\frac{10+6+15}{30\ \mu F}=\frac{31}{30\ \mu F}\)
\(\Leftrightarrow C_\mathrm{ges}=\frac{30}{31}\ \mu F=0,96774\ \mu F=967,74\ nF\)
2) \(C_1,C_2,C_3\) parallel zueinander
\(C_\mathrm{ges}=C_1+C_2+C_3=3\ \mu F+5\ \mu F+2\ \mu F=10\ \mu F=C_G\)
3) \(C_G\) in Reihe mit der Parallelschaltung von \(C_1, C_2, C_3\)
\(C_\mathrm{ges}=\frac{1}{C_G}+\frac{1}{C_G}=\frac{C_G\cdot C_G}{C_G+C_G}=\frac{10\ \mu F\cdot 10\ \mu F}{10\ \mu F+10\ \mu F}=5\ \mu F\)